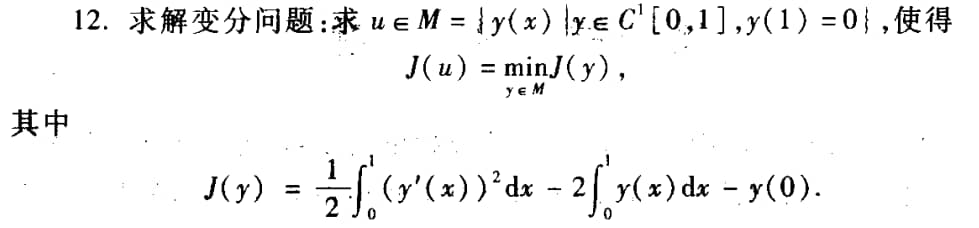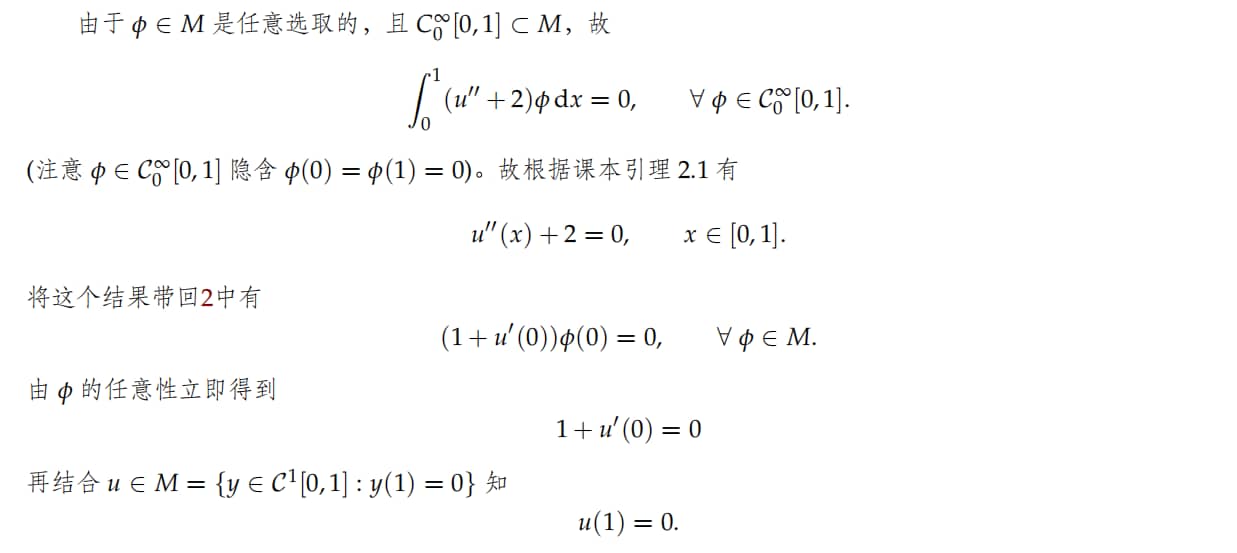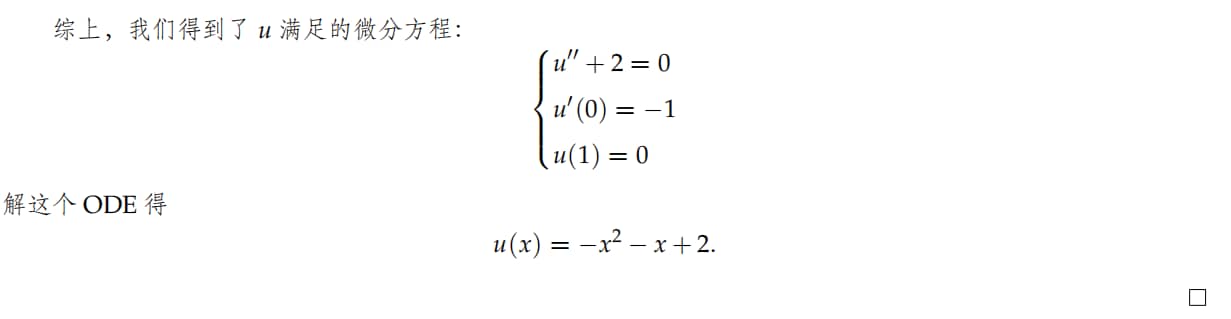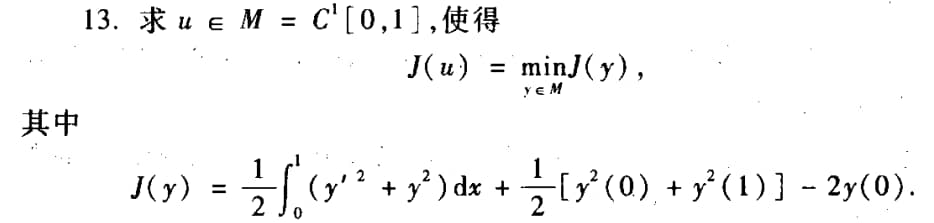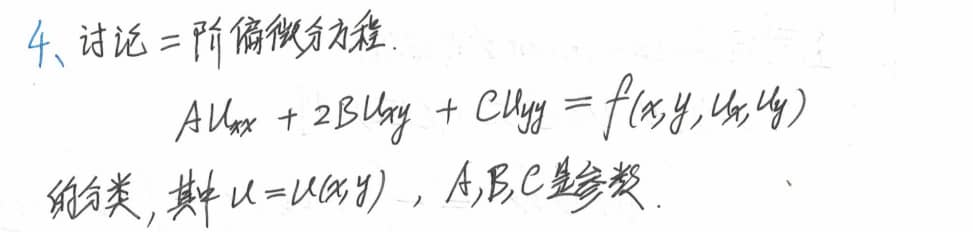本文最后更新于 2024年9月29日 下午
第一题
证明:
(1)
∫Ωuxivdx=−∫Ωu⋅vxidx+∫Ω∇xi(uv)dx=−∫Ωu⋅vxidx+∫∂Ωuv⋅nidS
(2)
∫ΩΔudx==∫Ω∇⋅(∇u)dx=∫∂Ω∇u⋅ndS∫∂Ω∂n∂udS
(3)
∫Ω∇u⋅∇vdx===−∫ΩuΔvdx+∫Ω∇(u⋅∇v)dx−∫ΩuΔvdx+∫∂Ωu∇v⋅ndS−∫ΩuΔvdx+∫∂Ωu∂n∂vdS
(4)
∫ΩuΔv−vΔudx===∫ΩuΔvdx−∫ΩvΔudx(∫∂Ωu∂n∂vdS−∫Ω∇u⋅∇vdx)−(∫∂Ωv∂n∂udS−∫Ω∇u⋅∇vdx)∫∂Ω(u∂n∂V−v∂n∂U)dS
第二题
T12
法1
(Fzk同学先教会了我T13的解法,我仿照T13的思路凑出了这个解法)
解: 由分部积分,
∫01(2x+1)y′dx+∫012ydx=(2x+1)y∣01=3⋅y(1)−y(0)=−y(0)
可得,
−∫012ydx=y(0)+∫01(2x+1)y′dx
代入得,
J(y)=21∫01(y′)2dx−2∫01ydx−y(0)=21∫01(y′)2dx+∫01(2x+1)y′dx+21∫01(2x+1)2dx−21∫01(2x+1)2dx=21∫01(y′+(2x+1))2dx−613≥−613
于是,
等号成立⇔{y′=−2x−1y(1)=0,∀x∈[0,1]⇔{y=−x2−x+c−1−1+c=0⇔u=−x2−x+2
法2
(解法 from Yjy同学)
T13
法1
(解法 from Fzk同学)
解:
首先,有分部积分,
∫01yy′dx=21y2∣01=21[y2(1)−y2(0)]
代入得,
J(y)=21∫01(y2+y2)dx+21[y2(0)+y2(1)]−2y(0)=21∫01(y+y′)2−2yy′dx+21[y2(0)+y2(1)]−2y(0)=21∫01(y+y′)2dx−∫01yy′dx+21[y2(0)+y2(1)]−2y(0)=21∫01(y+y′)2dx+y2(0)−2y(0)=21∫01(y+y′)2dx+(y(0)−1)2+1≥1
于是有,
等号成立⇔{y+y′=0y(0)=1,∀x∈[0,1]⇔{u′+u=0u(0)=1⇔u=e−x
法2
(解法 from Yjy同学)
T14
第一问
证明: 令
j(ϵ)=J(u+ϵv),v∈M.
则有,
j(ϵ)===J(u+ϵv)21∫Ω(∣∇(u+ϵv)∣2+(u+ϵv)2)dx+21∫∂Ωα(x)⋅(u+ϵv)2ds−∫Ωf(u+ϵv)dx−∫∂Ωg(u+ϵv)ds21∫Ω(∣∇u∣2+ϵ2∣∇v∣2+2ϵ⋅∇u⋅∇v+u2+2ϵuv+v2)dx+21∫∂Ωα(x)(u2+2ϵ⋅uv+ϵ2v2)ds−∫Ωf(u+ϵv)dx−∫∂Ωg(u+ϵv)ds
对 ϵ 求导,可得,
j′(ϵ)=∫Ω(ϵ∣∇v∣2+∇u⋅∇v+uv)dx+∫∂Ωα(x)(uv+ϵv2)ds−∫Ωfvdx−∫∂Ωgvds
于是,
问题1⇔j′(0)=0⇔∫Ω(∇u⋅∇v+uv−fv)dx+∫∂Ω(α(x)uv−gv)ds=0,∀v∈M⇔问题2
第二问
证明: 从第一问可得:问题1⇔问题2
于是只需证:
问题2⇔问题3
由 u∈C2(Ω)∪C1(Ω),使用分部积分以及 Gauss-Green 公式,
⇒∫Ω(∇u⋅∇v+v⋅Δu)dx=∫Ω∇(v⋅∇u)dx=∫∂Ωv⋅∇u⋅nds∫Ω∇u⋅∇vdx=∫∂Ωv∂n∂uds−∫ΩvΔudx
于是,
问题2⇔∫Ω(∇u⋅∇v+uv−fv)dx+∫∂Ω(α(x)uv−gv)ds=0,∀v∈M.⇔∫Ω(u−Δu−f)vdx+∫∂Ω(∂n∂u+α(x)u−g)vds,∀v∈M.⇔{−Δu+u=f∂n∂u+α(x)u=g,∀x∈Ω,∀x∈∂Ω⇔问题3
第三题
T16
第一问
证明: 由
∂t∂u=∂ξ∂u⋅∂t∂ξ+∂η∂u⋅∂t∂η=∂ξ∂u(−α)+∂η∂u(α)
有,
∂t2∂2u=∂t∂(−a∂ξ∂u+a∂η∂u)=(−a)(∂ξ2∂2u∂t∂ξ+∂η∂ξ∂2u∂t∂η)+a(∂η2∂2u∂t∂η+∂ξ∂η∂2u∂t∂ξ)=(−a)[∂ξ2∂2u(−a)+∂η∂ξ∂2u(a)]+a[∂η2∂2u(a)+∂ξ∂η∂2u(−a)]=a2(∂ξ2∂2u−2∂η∂ξ∂2u+∂η2∂2u)
又
∂x∂2u=∂ξ∂2u⋅∂x∂ξ+∂η∂2u⋅∂x∂η=∂ξ∂u+∂η∂u
得
∂x2∂2u=∂x∂(∂ξ∂u+∂η∂u)=(∂ξ2∂2u⋅∂x∂ξ+∂η∂ξ∂2u⋅∂x∂η)+(∂η2∂2u⋅∂x∂η+∂η∂ξ∂2u⋅∂x∂ξ)=∂ξ2∂2u+2∂η∂ξ∂2u+∂η2∂2u
代入 utt−a2⋅uxx=0,有:
a2(∂ξ02∂2u−2∂η∂ξ∂2u+∂η2∂2u)−a2(∂ξ2∂2u+2∂η∂ξ∂2u+∂η2∂2u)=0⇒∂η∂ξ∂2u=0
于是可得通解,
∫∂η∂ξ∂2udη=F1(ξ)⇒u=∫F1(ξ)dξ+G(η)=F(ξ)+G(η)⇒u(x,t)=F(x−at)+G(x+at)
第二问
证明: 首先,
∂t∂u=∂ξ∂u⋅∂t∂ξ+∂τ∂u⋅∂t∂τ=∂ξ∂u(−α)+∂τ∂u∂x∂u=∂ξ∂u⋅∂x∂ξ+∂τ∂u⋅∂x∂τ=∂ξ∂u∂x2∂2u=∂x∂(∂ξ∂2u)=∂ξ2∂2u⋅∂x∂ξ+∂τ∂ξ∂2u⋅∂x∂τ=∂ξ2∂2u
代入原式,
ut+αux=a2uxx⇔⇔(−α)uξ+uτ+α(uξ)=a2uξξuτ=a2uξξ
T17
证明: 首先,
∂xi∂u∂xi2∂2u=∂r∂u⋅∂xi∂r=u′⋅rxi=∂xi∂(u′⋅rxi)=∂r∂(u′⋅rxi)⋅∂xi∂r=(u′′⋅rxi+u′⋅r2r⋅xir−xi)⋅rxi=u′′⋅r2xi2+u′⋅r3r2−xi2
因此,
0=Δu=(i=1∑n∂xi2∂2)u=(i=1∑n∂xi2∂2)u=u′′⋅i=1∑nr2xi2+u′⋅i=1∑nr3r2−xi2=u′′+u′⋅rn−1
得到 u(r) 对应得常微分方程,
u′′+rn−1u′=0
第四题
解:
首先,考虑二阶项系数构成的矩阵之特征值,设特征值为 λ,则有,
A−λBBC−λ=(A−λ)(C−λ)−B2=λ2−(A+C)+(AC−B2)
由韦达定理,
{λ1+λ2=A+Cλ1λ2=AC−B2
上述方程的判别式为,
Δ=(A+C)2−4(AC−B2)=(A−C)2+4B2≥0
因此,λ1,λ2 都是实根。
情形一:两特征值全负
此时有,
{A+C<0AC−B2>0
在此情况下,上述二阶偏微分方程是椭圆型方程。
情形二:两特征值一0一负
此时有,
{A+C<0AC−B2=0
在此情况下,上述二阶偏微分方程是抛物型方程。
情形三:两特征值一正一负
此时有,
AC−B2<0
在此情况下,上述二阶偏微分方程是双曲型方程。
情形四:以上均不是
此时类型不为以上三种。